圆环转动惯量(圆环转动惯量怎么求)
如何计算环形物体的转动惯量?
dθ则圆环对直径的转动惯量JmR2/2π,宽,转动惯量,也就是内外径近似可以看做一个定值r则沿圆周,再设有两条相互垂直的直径。圆环转动惯量推导:在圆环内取一半径为r,宽度dr的圆环,其质量为dm=m/(πR2^2-πR1^2)*2πrdr,...,转动惯量为J=∫dJ。
可以先取一个宽度为dx的环形微元dm,计算环形微元相对于转轴的转动惯量,然后对整个圆盘从0到R对dx做积分。具体计算如下图。例:半径为R质量为M的圆盘,绕垂直于圆盘平面的质心轴转动,求转动惯量J。

直接用公式:L=Jw,其中L是就是所求刚体的角动量,J是刚体对转轴的转动惯量,w是转动角速度。在经典力学中,转动惯量(又称质量惯性矩,简称惯距)通常以I 或J表示,SI 单位为 kg·m。对于一个质点,I = mr,其中 m 是其质量,r 是质点和转轴的垂直距离。
三角形:I=b*h^3/36。圆形:I=π*d^4/64。环形:I=π*D^4*(1-α^4)/64;α=d/D。惯性矩通常被用作描述截面抵抗弯曲的性质。惯性矩的国际单位为(m4)。即面积二次矩,也称面积惯性矩,而这个概念与质量惯性矩(即转动惯量)是不同概念。
一个叫做“转动惯量”(也叫惯性矩),英文是Moment of Inertia,是一个用于描述物体旋转运动的物理量;一个叫做“截面惯量”(也叫截面矩,完整地说就是截面的惯性矩),英文实际应该是area moment of inertia,是一个用于描述截面几何性质的量,在材料力学中用于弯曲计算。
步进电机的惯量一般和启动频率有关系。一般情况下,启动和停止频率越高惯量越大,建议用低惯量马达或调低驱动电流,电压。长方体的物体如果是平放,接触的面就大,摩擦力就大。摩擦力是克服惯量的能力。摩擦力一般要大于步进电机的惯量物体才不会移动。
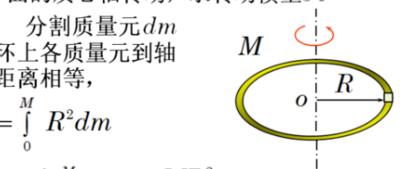
圆环绕直径的转动惯量怎么求,圆环绕中心轴的转动惯量怎么求,要详解...
圆环对直径的转动惯量求法,取微元dm= (m/2π)dθ,则圆环对直径的转动惯量:J=(mR/2π)∫sinθdθ 代入积分上限2π下限0积分可得:J=mR/2 圆环相当于一个空心的圆,空心圆拥有一个小半径(r),整个圆有一个大半径(R),整个圆的半径减去空心圆半径就是环宽。
根据转动惯量定义J=mr^2,然后用微元法分析,用微积分计算即可。积分参数为竖直夹角角度a。根据对称性,转动惯量是半圆的2倍。ds=rda。这个转动惯量是其实是一个常数,在角动量定理中 L=Jw.转动惯量有离散的求和形式和连续的积分形式。学过微积分马上就可以求出来。很简单。
在下圆盘上放上待测圆环,注意使圆环的质心恰好在转动轴上,测量系统的转动惯量。测量圆环的质量 和内、外直径 、 。利用式(14)求出圆环的转动惯量 。并与理论值进行比较,求出相对误差。圆环绕中心轴的转动惯量的理论值可由下式计算。式中 和 分别为圆环内、外直径。
转动惯量在转轴不变,质量不变的情况下,跟半径的平方成正比。角速度跟转动惯量成反比,所以跟半径的平方成反比。有角动量守恒,很容易得到。ω0/4 线没断时两球的转动惯量符合叠加原理。
转台旋转给油装置
紧凑性液压系统转台工作原理是通过电磁阀控制液压泵的启动,将压力输出到液压马达中,从而带动转台旋转,同时,通过液压油输出到液压缸中,控制转台的方向和角度,实现工程机械设备的各种工作任务。
该机械设备是油压。四轴液压转台使用液压系统作为动力源来驱动和控制转台的旋转运动。液压系统利用液压油作为工作介质,通过油泵将机械能转化为液压能,然后通过控制阀和油缸等液压元件将液压能传递到转台的旋转机构,从而实现转台的旋转运动。因此,四轴液压转台是油压的。
R-301系列,一款集高精度、动态卓越与工业设计美学于一体的360°连续旋转直驱转台,以其革命性的技术引领旋转控制领域。这款转台采用创新的旋转电机直驱设计,实现了定位精度高达±2角秒,重复性低至±1角秒的惊人水平,展现出了无与伦比的动态性能和稳定性。
升。通过查看小松360一7使用说明书,在小松360一7实现旋转功能需要加3升油。小松360一7是挖掘机的一种,机型配置大容量、高耐磨铲斗,其强化的动臂、斗杆和转台设计实现了工作中的强力挖掘和快速行走。
将制动活塞顶起,使制动摩擦片分离以解除制动,回转马达5方可通过回转减速器10驱动转台旋转。
求圆环的转动惯量
1、圆环转动惯量推导:在圆环内取一半径为r,宽度dr的圆环,其质量为dm=m/(πR2^2-πR1^2)*2πrdr,...,转动惯量为J=∫dJ。
2、圆环对直径的转动惯量求法,取微元dm= (m/2π)dθ,则圆环对直径的转动惯量:J=(mR/2π)∫sinθdθ 代入积分上限2π下限0积分可得:J=mR/2 圆环相当于一个空心的圆,空心圆拥有一个小半径(r),整个圆有一个大半径(R),整个圆的半径减去空心圆半径就是环宽。
3、圆环转动惯量推导:在圆环内取一半径为r,宽度dr的圆环,其质量为dm=m/(πR2^2-πR1^2)*2πrdr。对通过圆心垂直于圆平面轴的转动惯量为dJ=dmr^2=m/(πR2^2-πR1^2)*2πr^3dr。转动惯量为J=∫dJ。=∫(R1→R2)m/(πR2^2-πR1^2)*2πr^3dr。=1/2m(R2^2-R1^2)。
4、圆环的转动惯量是指圆环在转动时所受到的惯性力矩的大小,是转动系统运动状态的一个重要参数。转动惯量的大小取决于圆环的质量分布、质量分布的径向位置以及圆环的半径。对于一个质量均匀分布的圆环,其转动惯量可以根据公式 I = (m × R^2) / 2计算,其中 m 是圆环的质量,R 是圆环的半径。
5、圆环转动惯量的计算公式是基于牛顿第二定律推导出来的。根据牛顿第二定律,力的大小与物体的运动状态有关,而物体的运动状态可以用其质量和加速度来描述。当物体旋转时,其加速度可以表示为a = rα,其中α为角加速度,r为圆环的半径。因此,物体所受的合力F也可以表示为F = ma = mrα。
6、圆环的转动惯量是描述圆环绕轴线旋转时所拥有的惯性。它是刻画物体抗拒旋转运动的性质,类似于质点的质量,但用于描述物体的旋转运动。对于一个均匀密度的圆环来说,其转动惯量(也称为转动惯量、转动惯性)可以使用以下公式计算:I=mR。
圆环的转动惯量如何直接求解?
圆环对直径的转动惯量求法,取微元dm= (m/2π)dθ,则圆环对直径的转动惯量:J=(mR/2π)∫sinθdθ 代入积分上限2π下限0积分可得:J=mR/2 圆环相当于一个空心的圆,空心圆拥有一个小半径(r),整个圆有一个大半径(R),整个圆的半径减去空心圆半径就是环宽。
圆环转动惯量推导:在圆环内取一半径为r,宽度dr的圆环,其质量为dm=m/(πR2^2-πR1^2)*2πrdr,...,转动惯量为J=∫dJ。
圆环转动惯量的计算公式是基于牛顿第二定律推导出来的。根据牛顿第二定律,力的大小与物体的运动状态有关,而物体的运动状态可以用其质量和加速度来描述。当物体旋转时,其加速度可以表示为a = rα,其中α为角加速度,r为圆环的半径。因此,物体所受的合力F也可以表示为F = ma = mrα。
对于一个绕着直径旋转的圆环,它的转动惯量可以分解为两部分:一个是围绕圆环中心的转动惯量,另一个是围绕圆环直径的转动惯量。根据叠加原理,它们的和就是圆环对直径的总转动惯量。
求解圆环的转动惯量,需要使用公式 I = mR^2,其中 I 是转动惯量,m 是圆环的质量,R 是圆环的半径。转动惯量是物体在转动时的惯性量度,它描述了物体对转动的抵抗程度。对于圆环,其转动惯量与其质量、半径的平方成正比。因此,要求解圆环的转动惯量,需要知道圆环的质量和半径。
圆环的转动惯量
1、圆环转动惯量推导:在圆环内取一半径为r,宽度dr的圆环,其质量为dm=m/(πR2^2-πR1^2)×2πrdr,……,转动惯量为J=∫dJ。转动惯量是刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。在经典力学中,转动惯量通常以I或J表示,SI单位为kg·m。
2、圆环对直径的转动惯量求法,取微元dm= (m/2π)dθ,则圆环对直径的转动惯量:J=(mR/2π)∫sinθdθ 代入积分上限2π下限0积分可得:J=mR/2 圆环相当于一个空心的圆,空心圆拥有一个小半径(r),整个圆有一个大半径(R),整个圆的半径减去空心圆半径就是环宽。
3、圆环转动惯量推导:在圆环内取一半径为r,宽度dr的圆环,其质量为dm=m/(πR2^2-πR1^2)*2πrdr,...,转动惯量为J=∫dJ。
4、圆环的转动惯量是描述圆环绕轴线旋转时所拥有的惯性。它是刻画物体抗拒旋转运动的性质,类似于质点的质量,但用于描述物体的旋转运动。对于一个均匀密度的圆环来说,其转动惯量(也称为转动惯量、转动惯性)可以使用以下公式计算:I=mR。
5、圆环转动惯量的计算公式是基于牛顿第二定律推导出来的。根据牛顿第二定律,力的大小与物体的运动状态有关,而物体的运动状态可以用其质量和加速度来描述。当物体旋转时,其加速度可以表示为a = rα,其中α为角加速度,r为圆环的半径。因此,物体所受的合力F也可以表示为F = ma = mrα。







































